1、前言
甲醇廠空分車間液氨儲罐液位測量儀表設(shè)計選用P+H雷達液位計。2009年投入運行后,因回波對測量波干擾強度無法消除,導(dǎo)致雷達液位計顯示值波動較大,不能滿足廠工藝*監(jiān)控要求;2010年該儲罐液位測量儀表改用了雙法蘭式差壓變送器,但在實際使用中,發(fā)現(xiàn)該差壓變送器指示值與實際液位仍有較大偏差,仍然不能滿足工藝過程的*控制和監(jiān)視要求。為此,對現(xiàn)場工藝指標(biāo)進行了大量數(shù)據(jù)收集和系統(tǒng)的分析,找出了導(dǎo)致實際值與顯示值存在較大偏差的根本原因,并提出了切實可行的解決方案,大大降低了測量誤差,達到了工藝監(jiān)測和控制的要求。
2、測量誤差原因分析
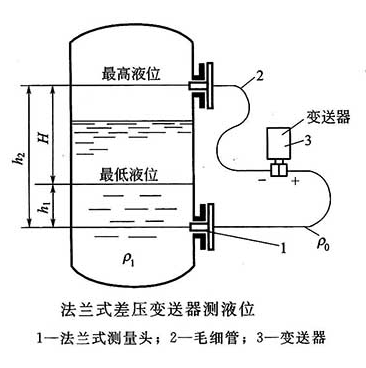
甲醇廠使用的差壓液位變送器,是依據(jù)液體靜壓力原理和液體連通器原理來計算和測量液位的。其將一個空間用敏感元件(多用膜盒),分割成兩個不同的腔室,如果分別向正壓腔室和負壓腔室引入不同的壓力時,差壓液位變送器傳感器在正壓腔壓力和負壓腔壓力的共同作用下產(chǎn)生位移(或位移的趨勢),這個位移量和兩個腔室壓力的差(差壓)成正比,差壓液位變送器的變送單元裝置,將這種位移量轉(zhuǎn)換成可以反映差壓大小的標(biāo)準(zhǔn)信號(一般是電流為4~20mA直流信號)進行輸出,DCS控制系統(tǒng)(或二次儀表)通過接收差壓式液位變送器輸出的標(biāo)準(zhǔn)信號,然后按照接收到的標(biāo)準(zhǔn)信號的大小和測量液體的密度,計算出被測液體的實際液位。其測量原理如圖1所示。
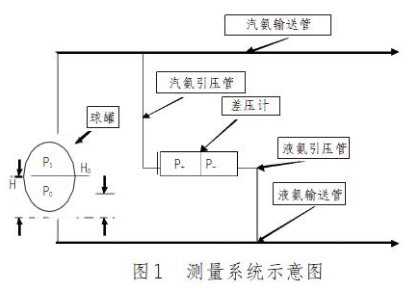
由液體靜壓力原理得:
H=(P0-P1)/ρ液(1)
由液體連通器原理得;
P0=P++H0×ρ液(2)
P1=P--(H-H0)×ρ汽(3)
其中,H為儲罐液位,H0為差壓式液位變送器安裝位置距儲罐底部的距離,P1為儲罐內(nèi)部液體表面靜壓,P0為儲罐內(nèi)液體本身產(chǎn)生的壓力,ρ液為儲罐內(nèi)部液體的密度,ρ汽為儲罐內(nèi)部氣體的密度,P+為差壓式變送器正壓腔室內(nèi)部壓力,P-為差壓式變送器負壓腔室內(nèi)部壓力。
將式(2)、式(3)代入式(1)整理后可得:
H=△P/(ρ液-ρ汽)+H0(4)
由式(4)可以分析出,影響儲罐液位測量高度是否*的因素,不僅取決與差壓式位變送器測量的差壓值△P,還取決與被測量液體汽液相密度的差(ρ液-ρ汽)和差壓式變送器實際安裝的高度H0。同時被測液體汽液相密度差(ρ液-ρ汽),是隨著介質(zhì)溫度而變化,但差壓式液位變送器本身對這些因素是無法測量的,差壓式變送器本身在計算液位高度值H時,采用的是(ρ液-ρ汽)的測量值。這樣,必然會造成液體實際液位高度值和儀表測量指示值之間的偏差。同時,由于被測液體實際溫度和壓力的變化,在汽氨的導(dǎo)壓管路中,也會使汽氨液化,從而產(chǎn)生不同高度的液柱(不同高度的液柱將產(chǎn)生不同的壓力),進而影響測量的精度。
設(shè)導(dǎo)壓管內(nèi)液化產(chǎn)生液柱的高度為H1,則原(3)式、(4)式應(yīng)修正為:
P1=P-(H-H0)×ρ汽-(H-H1-H0)×ρ汽(5)
H=△P/(ρ液-ρ汽)+H0+H0+H1(6)
在測量中,由于H1的實際值無法測量(同時H1也和安裝高度、環(huán)境溫度以及維護人員素質(zhì)有關(guān))而經(jīng)常被忽略不計,這必然會造成實際液位高度值和儀表指示值之間的偏差。zui后,儀表本身的制造精度,也會造成不同程度的測量偏差。綜上所述,甲醇廠液氨儲罐液位測量偏差的主要來源包括:被測液氨實際溫度和壓力的變化、汽氨引壓管路中液柱的高度,以及儀表制造精度本身的測量偏差。
3、糾偏方案
3.1對液氨實際溫度變化的補償方案
要降低被測介質(zhì)的實際溫度變化對液位測量精度的影響,目前常常采用以下兩種方案:①對被測介質(zhì)進行保溫,保證被測介質(zhì)溫度保持相對恒定。②對被測介質(zhì)溫度進行實時測量,對被測介質(zhì)溫度變化引起的測量偏差進行補償。方案一工程量較大,造價高,而且由于環(huán)境溫度、工藝控制等不同因素的影響,很難保證在生產(chǎn)過程中介質(zhì)溫度的**恒定;方案二的工程量小(僅安裝一套測溫變送儀表即可),雖然需要進行非常繁瑣的計算,但是在原有的DCS控制系統(tǒng)中卻是很容易實現(xiàn)的。因此,選用方案二進行補償。
要實現(xiàn)對被測液體溫度變化引起的液位偏差進行補償,**要明確測量介質(zhì)(氨)的密度隨溫度變化的函數(shù)關(guān)系:ρ液=F(T)和ρ汽=f(T),二是根據(jù)液體的靜壓力原理和連通器原理,求出液體實際高度計算公式:即h=H(T,△P),zui后修改DCS控制系統(tǒng)程序,用已測量出介質(zhì)的實時溫度和液差壓式液位變送器測量出的差壓值,計算出儲罐中氨的實際液位高度值。
3.1.1氨的密度與溫度之間函數(shù)關(guān)系式的確定
目前,被測介質(zhì)氨的密度與溫度之間的函數(shù)關(guān)系,很難用非常準(zhǔn)確的數(shù)學(xué)模型來表示,但氨這種介質(zhì)在飽和狀態(tài)下的密度與溫度之間的關(guān)系是一定的,在一定的溫度范圍內(nèi),完全可以用統(tǒng)計分析等相關(guān)技術(shù),來擬合出一條近似的曲線來表示它們之間的關(guān)系。表1列出的是在0℃~30℃的溫度范圍內(nèi),介質(zhì)氨在飽和狀態(tài)下的密度與溫度之間的對應(yīng)的關(guān)系。
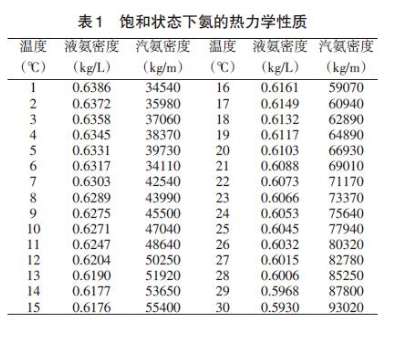
為了進一步分析被測介質(zhì)氨的密度與溫度之間的對應(yīng)關(guān)系,根據(jù)表1的數(shù)據(jù),描出了汽氨和液氨的密度—溫度關(guān)系散點圖,見圖2。
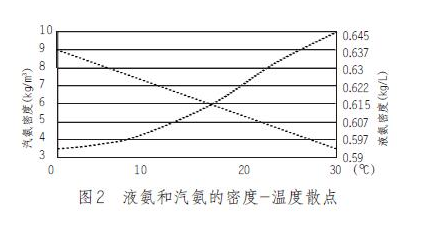
從圖2可以看出:在一定的溫度范圍內(nèi),被測介質(zhì)氨的密度與溫度有很密切的相關(guān)性,即汽氨的密度與溫度的函數(shù)關(guān)系,可以近似為指數(shù)函數(shù)關(guān)系,而液氨的密度與溫度則是線性相關(guān)。
為了進一步得到氨的密度與溫度之間變化的*數(shù)學(xué)模型,利用Excel軟件提供的函數(shù)公式,依據(jù)表1列出的數(shù)據(jù),對液氨的密度與溫度之間的關(guān)系進行線性回歸。同時,對汽氨的密度與溫度的關(guān)系進行指數(shù)回歸,可以得出如下關(guān)系式:
ρ液=0.639-0.00145×t(7)
ρ汽=3.5125×1.0324t(8)
3.1.2函數(shù)關(guān)系回歸偏差的排除
為了降低數(shù)學(xué)模型回歸本身帶來的偏差,假設(shè)△P、H1、H0均為常數(shù),且H1、H0均為零。這樣,由(6)式得:H=△P/(ρ液-ρ汽)(9)
數(shù)學(xué)模型回歸本身引起的偏差即為:
△H=△P/(ρ液-ρ汽)-△P/(ρ液標(biāo)-ρ汽標(biāo))(10)其中:ρ液、ρ汽為某一特定溫度下氨的數(shù)學(xué)模型回歸密度值,ρ液標(biāo)、ρ汽標(biāo)為該溫度下氨的實際密度值。將(10)式除以(9)式得:
△H/H=1-(ρ液-ρ汽)(/ρ液標(biāo)-ρ汽標(biāo))(11)
在0℃~30℃范圍內(nèi),儲罐中氨的存在形式往往不會真正處于飽和狀態(tài),汽氨的實際溫度往往會高于液氨的實際溫度(zui高差距有時可達到10℃以上)。當(dāng)汽氨的實際溫度變化時,其密度也會產(chǎn)生相應(yīng)的變化。因此,如果用飽和狀態(tài)下的液氨溫度,來計算汽氨當(dāng)前的密度,會引起測量的偏差。因此在計算中,當(dāng)液氨的實際溫度為15℃時,(10)式中的ρ液標(biāo)應(yīng)取t=(10+15)℃時相對應(yīng)的溫度值。此時,△H/H=-0.0429%。由此可以看出:在此溫度范圍內(nèi),氨的數(shù)學(xué)模型擬合過程本身引起的zui大正偏差為0.070%,zui大負偏差為0.0429%,這個偏差小到可以忽略不計的程度。因此,按照以上方案擬合的數(shù)學(xué)模型,相對準(zhǔn)確地再現(xiàn)了氨的密度與溫度之間的函數(shù)關(guān)系。
3.1.3儲罐液位的計算
將(7)式、(8)式代入(6)式可得:
H=△P/(0.639-0.00145×t-3.5125×1.0324t)-H0-H1(12)
按照上式計算出的液氨液位,基本上可以消除實際生產(chǎn)過程中現(xiàn)場實時溫度變化,對液位測量的影響。消除液柱引起的偏差有兩個方案:**可以在汽氨導(dǎo)壓管的zui高點加一隔離罐,使式(6)中的H1為一常數(shù);二是取消差壓液位變送器,直接采用壓力變送器,測量儲罐頂部的汽氨壓力和儲罐底部的液氨壓力來計算液位。方案二可以直接利用現(xiàn)已安裝的壓力變送器,不需要再增加設(shè)備,只需要在現(xiàn)有的DCS控制系統(tǒng)中,改變原有的組態(tài)就可以實現(xiàn)。因此,選用了二種方案。
根據(jù)液體的靜壓力原理和液體的連通器原理得:
H=(P0-P1)/ρ液(13)
P0=P液-H0×ρ液(14)
P1=P汽+(H1-H)×ρ汽(15)
將(10)式、(11)式帶入(9)式:
H=(P液-P汽)(/ρ液-ρ汽)-H0-(H1+H0)×ρ汽(/ρ液-ρ汽)(16)將(7)式、(8)式帶入(12)式,求出的液位計算公式為:
H=(P液-P汽)(/0.639-0.00145×t-0.0035125×1.0324t)-H0-(H1+H0)×0.0035125×1.0324(t/0.639-0.00145×t-0.0035125×1.0324t)(17)
其中,P液為液氨壓力的實際測量值,P汽為汽氨壓力的實際測量值,H1為液氨壓力變送器安裝位置距液氨儲罐底部的距離,H0為汽氨壓變送器表安裝位置距液氨儲罐底部的距離,t為被測介質(zhì)氨在飽和狀態(tài)下的實際溫度值。從(17)式可以看出,儲罐液氨實際高度H的大小取決于P液、P汽、H1、t和H0的值,壓力變送器的安裝高度H1、和H0的值是固定不變的,t是現(xiàn)有DCS控制系統(tǒng)中已經(jīng)測量到的變量值。
4、結(jié)論
本論文找出了導(dǎo)致甲醇廠液氨儲罐液位,在實際測量過程中存在較大偏差的根本原因,并提出了切實可行的溫度和液柱補償糾偏方案,采用差壓液位變送器進行液位計測量方案,基本消除了液氨實際溫度變化和液柱高度等不確定因素,對測量精度的影響,達到了液氨儲罐液位*監(jiān)測和控制的要求。同時,對解決同行業(yè)、同類相關(guān)介質(zhì)液位的*測量問題,提供了理論思路。
華恒資訊:磁翻板液位計和磁致伸縮液位計的區(qū)別
華恒資訊:磁翻板液位計和磁致伸縮液位計的區(qū)別


 當(dāng)前位置:
當(dāng)前位置:




